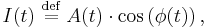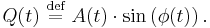Phase (waves)
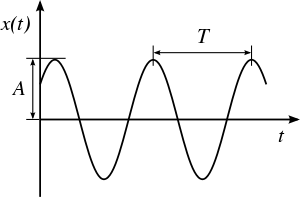
The phase of an oscillation or wave is the fraction of a complete cycle corresponding to an offset in the displacement from a specified reference point at time t = 0. Phase is a frequency domain or Fourier transform domain concept, and as such, can be readily understood in terms of simple harmonic motion. The same concept applies to wave motion, viewed either at a point in space over an interval of time or across an interval of space at a moment in time. Simple harmonic motion is a displacement that varies cyclically, as depicted to the right.
It is described by the formula:
where A is the amplitude of oscillation, f is the frequency, t is the elapsed time, and 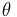 is the phase of the oscillation. The phase determines or is determined by the initial displacement at time t = 0. A motion with frequency f has period
is the phase of the oscillation. The phase determines or is determined by the initial displacement at time t = 0. A motion with frequency f has period 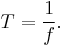
Two potential ambiguities can be noted:
- The initial displacement of
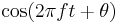 is different from the sine function, yet they appear to have the same "phase".
is different from the sine function, yet they appear to have the same "phase". - The time-variant angle
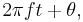 or its modulo
or its modulo  value, is also commonly referred to as "phase". Then it is not an initial condition, but rather a continuously-changing condition.
value, is also commonly referred to as "phase". Then it is not an initial condition, but rather a continuously-changing condition.
The term instantaneous phase is used to distinguish the time-variant angle from the initial condition. It also has a formal definition that is applicable to more general functions and unambiguously defines a function's initial phase at t=0. I.e., sine and cosine inherently have different initial phases. When not explicitly stated otherwise, cosine should generally be inferred. (also see phasor)
Contents |
Phase shift
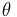 is sometimes referred to as a phase-shift, because it represents a "shift" from zero phase. But a change in
is sometimes referred to as a phase-shift, because it represents a "shift" from zero phase. But a change in 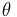 is also referred to as a phase-shift.
is also referred to as a phase-shift.
For infinitely long sinusoids, a change in 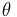 is the same as a shift in time, such as a time-delay. If
is the same as a shift in time, such as a time-delay. If 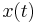 is delayed (time-shifted) by
is delayed (time-shifted) by 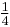 of its cycle, it becomes:
of its cycle, it becomes:
whose "phase" is now 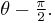 It has been shifted by
It has been shifted by 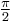 .
.
Phase difference
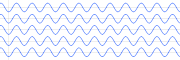


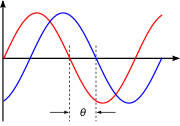
Two oscillators that have the same frequency and different phases have a phase difference, and the oscillators are said to be out of phase with each other. The amount by which such oscillators are out of step with each other can be expressed in degrees from 0° to 360°, or in radians from 0 to 2π. If the phase difference is 180 degrees (π radians), then the two oscillators are said to be in antiphase. If two interacting waves meet at a point where they are in antiphase, then destructive interference will occur. It is common for waves of electromagnetic (light, RF), acoustic (sound) or other energy to become superposed in their transmission medium. When that happens, the phase difference determines whether they reinforce or weaken each other. Complete cancellation is possible for waves with equal amplitudes.
Time is sometimes used (instead of angle) to express position within the cycle of an oscillation.
- A phase difference is analogous to two athletes running around a race track at the same speed and direction but starting at different positions on the track. They pass a point at different instants in time. But the time difference (phase difference) between them is a constant - same for every pass since they are at the same speed and in the same direction. If they were at different speeds (different frequencies), the phase difference is undefined and would only reflect different starting positions. Technically, phase difference between two entities at various frequencies is undefined and does not exist.
- Time zones are also analogous to phase differences.
In-phase and quadrature (I&Q) components
The term in-phase is also found in the context of communication signals:
and:
where 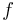 represents a carrier frequency, and
represents a carrier frequency, and
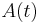 and
and 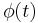 represent possible modulation of a pure carrier wave, e.g.:
represent possible modulation of a pure carrier wave, e.g.: 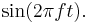 The modulation alters the original
The modulation alters the original 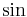 component of the carrier, and creates a (new)
component of the carrier, and creates a (new) 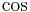 component, as shown above. The component that is in phase with the original carrier is referred to as the in-phase component. The other component, which is always 90° (
component, as shown above. The component that is in phase with the original carrier is referred to as the in-phase component. The other component, which is always 90° (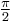 radians) "out of phase", is referred to as the quadrature component.
radians) "out of phase", is referred to as the quadrature component.
Phase coherence
Coherence is the quality of a wave to display well defined phase relationship in different regions of its domain of definition.
In physics, quantum mechanics ascribes waves to physical objects. The wave function is complex and since its square modulus is associated with the probability of observing the object, the complex character of the wave function is associated to the phase. Since the complex algebra is responsible for the striking interference effect of quantum mechanics, phase of particles is therefore ultimately related to their quantum behavior.
Phase compensation
Phase compensation is the correction of phase error (i.e., the difference between the actually needed phase and the obtained phase). A phase compensation is required to obtain stability in an opamp. A capacitor/RC network is usually used in the phase compensation to keep a phase margin. A phase compensator subtracts out an amount of phase shift from a signal which is equal to the amount of phase shift added by switching one or more additional amplifier stages into the amplification signal path.
See also
- Instantaneous phase
- Lissajous curve
- Phase cancellation
- Polarity
- Polarization
External links
- Relationship of phase difference and time-delay
- Phase angle, phase difference, time delay, and frequency
- ECE 209: Sources of Phase Shift — Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
- Phase Difference Java Applet
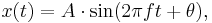
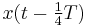
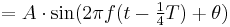
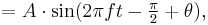
![A(t)\cdot \sin[2\pi ft + \phi(t)]
= I(t)\cdot \sin(2\pi ft) + Q(t)\cdot \underbrace{\cos(2\pi ft)}_{\sin\left(2\pi ft + \frac{\pi}{2} \right)}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/495c56a3fbdb8d025f18c8662f9c25bd.png)
![A(t)\cdot \cos[2\pi ft + \phi(t)]
= I(t)\cdot \cos(2\pi ft) \underbrace{{}- Q(t)\cdot \sin(2\pi ft)}_{{} + Q(t)\cdot \cos\left(2\pi ft + \frac{\pi}{2}\right)},](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/13cdb6461af35407231f182994d4a290.png)